Algorithms, Part II - Week 3 - Baseball Elimination

发表于 2017-12-04 分类于 MOOC

一个计算球队是否能拿冠军的算法，但要是看到被算出局后，教练和球员肯定是不信的

分析

这题评分有点怪，正确读入数据后主要的算法函数没写也能过，其实算法代码量很短，但不可能第一眼就有灵感，讲义信息量也很巨大

	w[i]	l[i]	r[i]
i	team	wins	loss	left	Atl	Phi	NY
0	Atlanta	83	71	8	-	1	6
1	Philadelphia	80	79	3	1	-	0
2	New York	78	78	6	6	0	-
3	Montreal	77	82	3	1	2	0

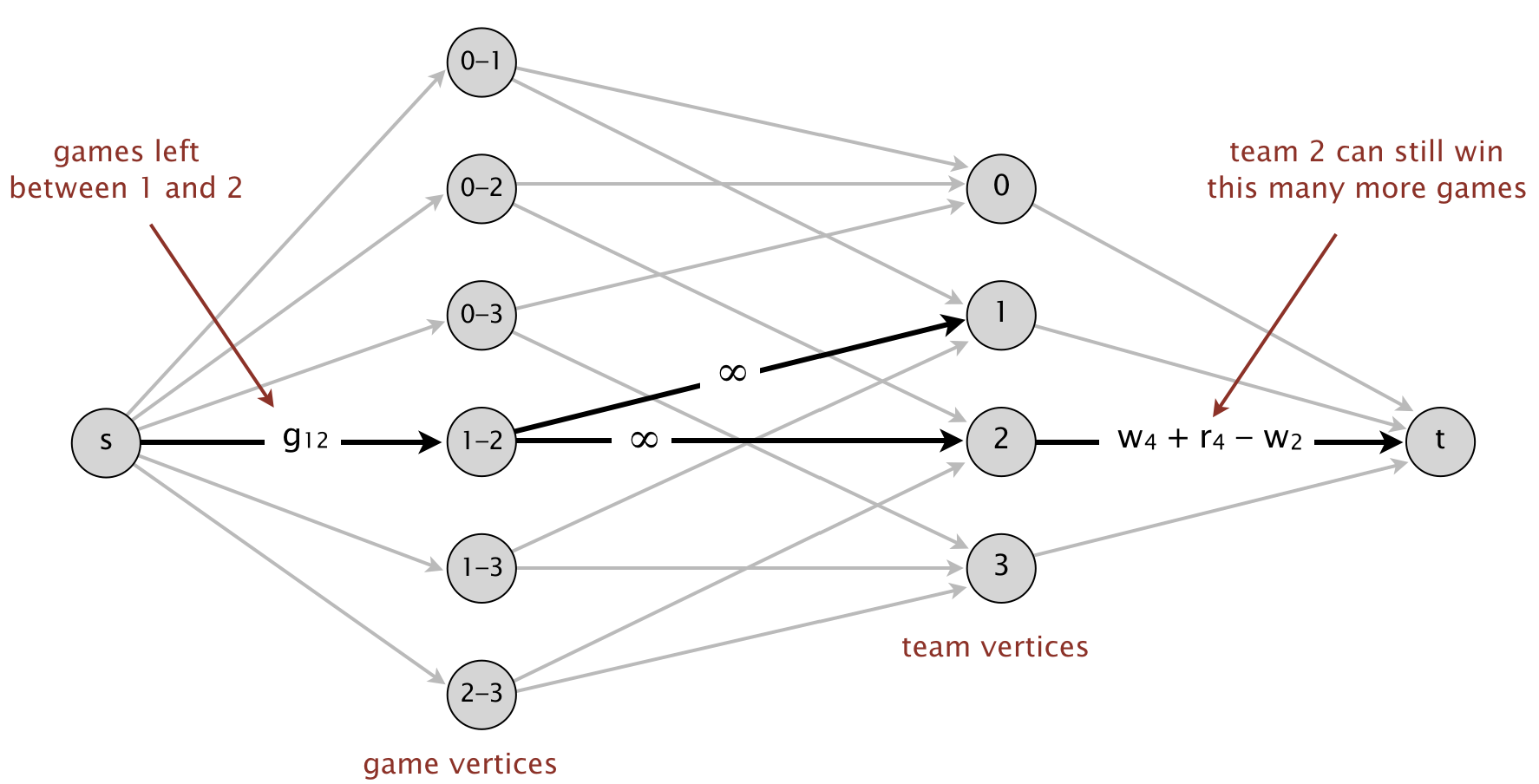
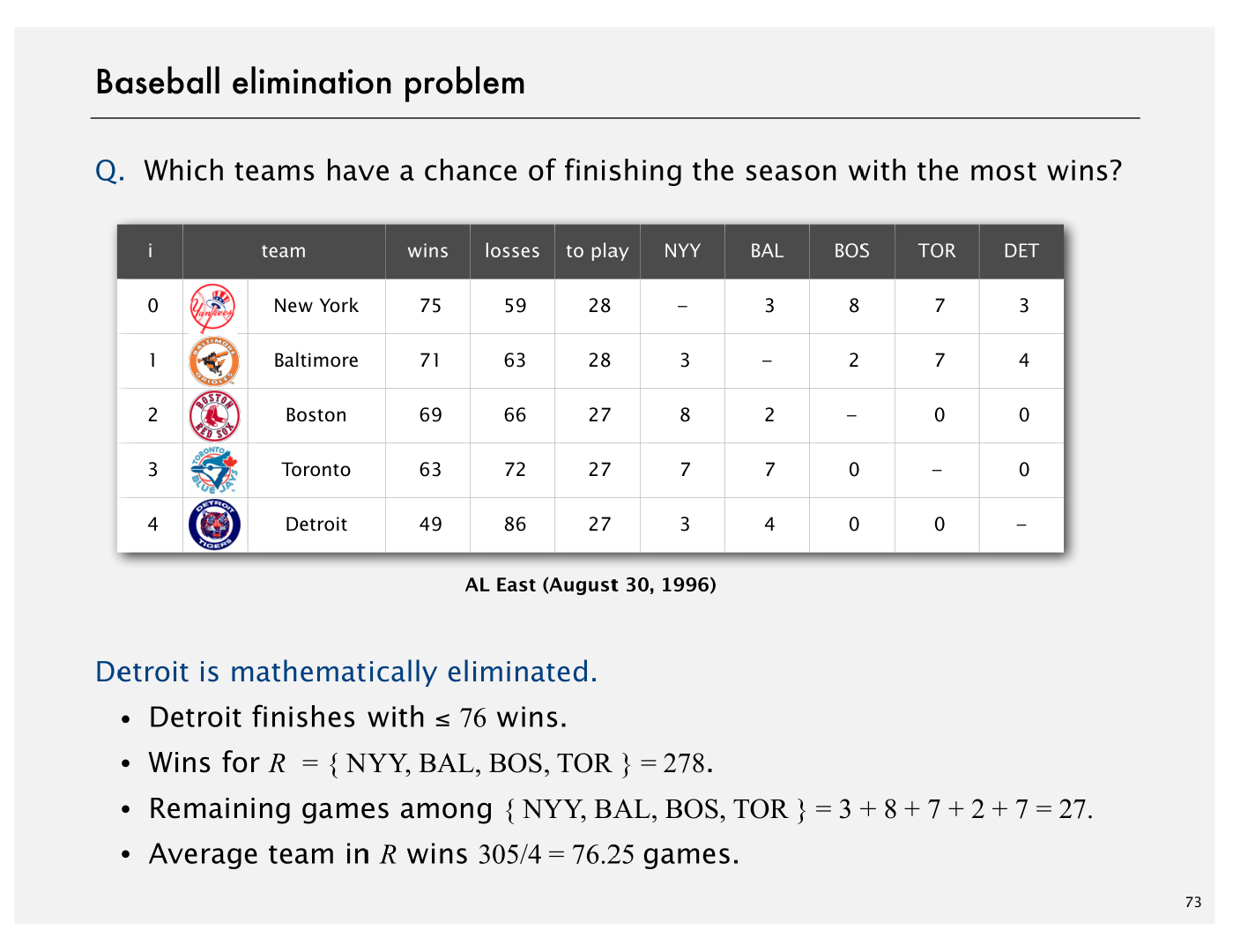
Montreal is mathematically eliminated since it can finish with at most 80 wins and Atlanta already has 83 wins. This is the simplest reason for elimination. However, there can be more complicated reasons. For example, Philadelphia is also mathematically eliminated. It can finish the season with as many as 83 wins, which appears to be enough to tie Atlanta. But this would require Atlanta to lose all of its remaining games, including the 6 against New York, in which case New York would finish with 84 wins. We note that New York is not yet mathematically eliminated despite the fact that it has fewer wins than Philadelphia.

读入wins[i]， losses[i]， remain[i]，以及 games[i][j]，要注意存要考虑读只有一个球队的数据

isEliminated()

一个按照公式的暴力计算方法

certificateOfElimination()

0%