Algorithms, Part I - Week 1 - Percolation
来自 Coursera 上普林斯顿大学的 Algorithms, Part I 课程的第一周编程作业Percolation
分析
渗流。在一个多孔地表表层有水(或地下有石油),判断在什么条件下, 水能够流失到底部(或石油涌出到地表)。科学家已经定义了一个被称为渗流的抽象过程来模拟这种情况。
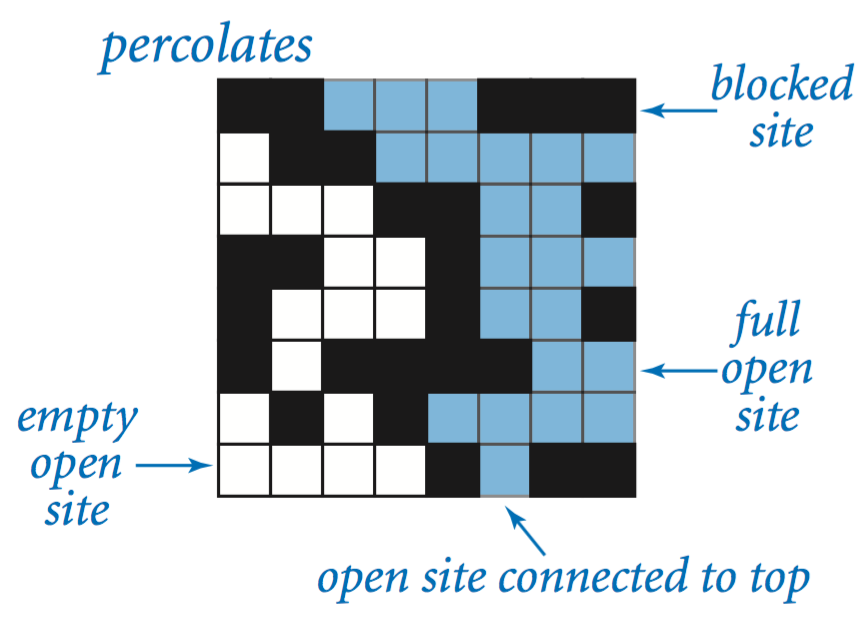
给定一个 n 乘 n 的网格,每块以概率 p 打开,当且仅当顶部到底部被打开的块相连接时,称这个系统为渗流的
 |
 |
|---|---|
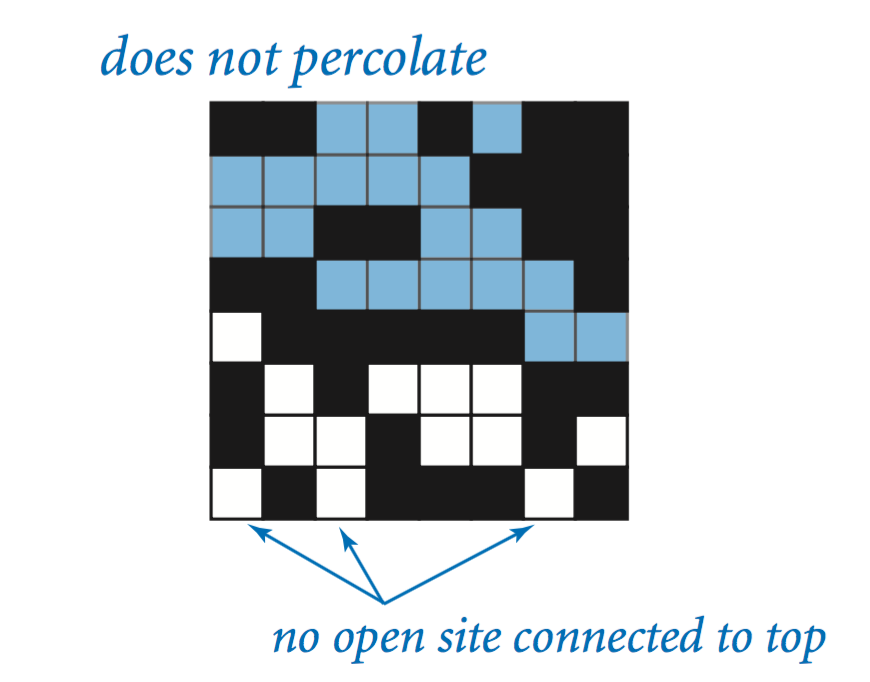
| 渗流 | 不渗流 |
当边长 n 很大时,有一个阈值 p*
- p > p* 很可能渗流
- p < p* 很可能不渗流
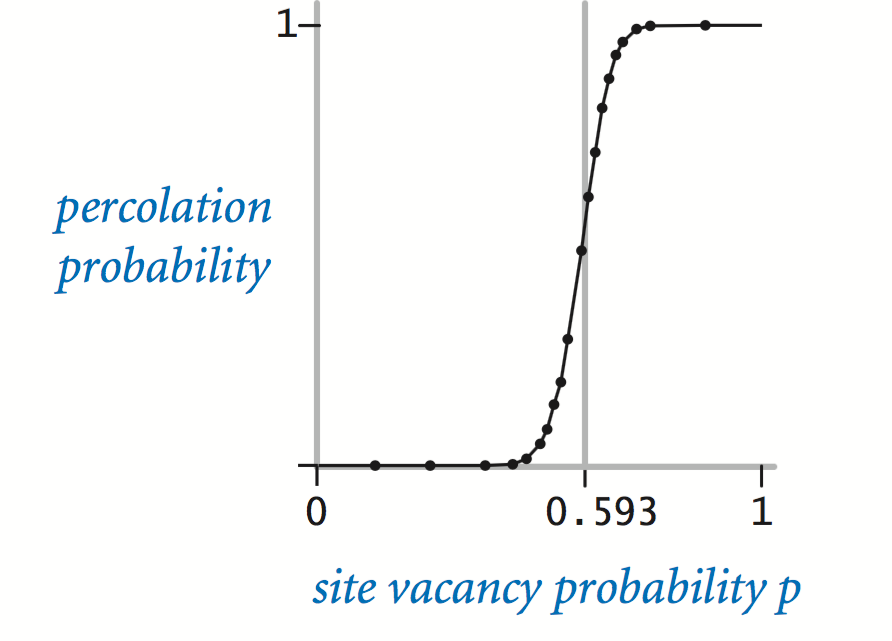
这个作业的任务就是估算这个阈值 p*
测试
课程提供 Visualization client 和 InteractiveVisualization client 进行测试,具体查看Checklist
解答
使用课程提供的 algs4.jar 的 StdIn, StdOut, StdRandom, StdStats, WeightedQuickUnionUF 库函数完成两个类文件
Percolation data type. To model a percolation system, create a data type Percolation with the following API:
public class Percolation {
public Percolation(int n) // create n-by-n grid, with all sites blocked
public void open(int row, int col) // open site (row, col) if it is not open already
public boolean isOpen(int row, int col) // is site (row, col) open?
public boolean isFull(int row, int col) // is site (row, col) full?
public int numberOfOpenSites() // number of open sites
public boolean percolates() // does the system percolate?
public static void main(String[] args) // test client (optional)
}To perform a series of computational experiments, create a data type PercolationStats with the following API.
public class PercolationStats {
public PercolationStats(int n, int trials) // perform trials independent experiments on an n-by-n grid
public double mean() // sample mean of percolation threshold
public double stddev() // sample standard deviation of percolation threshold
public double confidenceLo() // low endpoint of 95% confidence interval
public double confidenceHi() // high endpoint of 95% confidence interval
public static void main(String[] args) // test client (described below)
}答案
Percolation.java
import javax.swing.plaf.synth.Region;
import javax.xml.ws.EndpointReference;
import edu.princeton.cs.algs4.WeightedQuickUnionUF;
public class Percolation {
private int n;
private int countOpen = 0;
private boolean[][] grid;
private WeightedQuickUnionUF uf;
private WeightedQuickUnionUF uf1;
// create n-by-n grid, with all sites blocked
public Percolation(int n)
{
if (n < 1)
{
throw new java.lang.IllegalArgumentException();
}
this.n = n;
grid = new boolean[n+1][n+1];
uf = new WeightedQuickUnionUF(n*n + 2); // pdf 58
uf1 = new WeightedQuickUnionUF(n*n + 1);
}
// open site (row, col) if it is not open already
public void open(int row, int col)
{
if (row < 1 || col < 1 || row > n || col > n)
{
throw new java.lang.IndexOutOfBoundsException();
}
if(!isOpen(row, col))
{
// first row
if (row == 1)
{
uf.union(0, col);
uf1.union(0, col);
}
// last row
if (row == n)
{
uf.union(n * n + 1, (row - 1) * n + col);
}
// else, set this site open
grid[row][col] = true;
countOpen++;
System.out.println("*-"+countOpen+"-*");
System.out.println("*-"+numberOfOpenSites()+"-*");
///// and see if its neighbors is full ////
// left neighbor
if (col > 1 && isOpen(row, col-1))
{
uf.union((row-1) * n + col, (row-1) * n + col - 1);
uf1.union((row-1) * n + col, (row-1) * n + col - 1);
}
// right neighbor
if (col < n && grid[row][col+1])
{
uf.union((row-1) * n + col, (row-1) * n + col + 1);
uf1.union((row-1) * n + col, (row-1) * n + col + 1);
}
// up neighbor
if (row > 1 && isOpen(row-1, col))
{
uf.union((row-1) * n + col, (row-2) * n + col);
uf1.union((row-1) * n + col, (row-2) * n + col);
}
// down neighbor
if (row < n && isOpen(row+1, col))
{
uf.union((row-1) * n + col, row * n + col);
uf1.union((row-1) * n + col, row * n + col);
}
}
}
// is site (row, col) open?
public boolean isOpen(int row, int col)
{
if (row < 1 || col < 1 || row > n || col > n)
{
throw new java.lang.IndexOutOfBoundsException();
}
if (grid[row][col])
{
return true;
}
else
{
return false;
}
}
// is site (row, col) full?
public boolean isFull(int row, int col)
{
if (row < 1 || col < 1 || row > n || col > n)
{
throw new java.lang.IndexOutOfBoundsException();
}
if (grid[row][col])
{
if (uf1.connected(0, (row-1) * n + col))
{
return true;
}
}
return false;
}
// number of open sites
public int numberOfOpenSites()
{
return countOpen;
}
// does the system percolate?
public boolean percolates()
{
return uf.connected(0, n * n + 1);
}
}PercolationStats.java
import edu.princeton.cs.algs4.StdRandom;
import edu.princeton.cs.algs4.StdStats;
public class PercolationStats {
private double[] results;
private int count = 0;
private double mean = 0;
private double stddev = 0;
private double confidenceHi = 0;
private double confidenceLo = 0;
private Percolation perc;
// perform trials independent experiments on an n-by-n grid
public PercolationStats(int n, int trials)
{
if (n <= 0 || trials <= 0)
{
throw new java.lang.IllegalArgumentException();
}
results = new double[trials];
for (int i = 0; i < trials; i++, count = 0)
{
perc = new Percolation(n);
while (!perc.percolates())
{
int row = StdRandom.uniform(n)+1;
int col = StdRandom.uniform(n)+1;
while (perc.isOpen(row, col))
{
// regenerate random
row = StdRandom.uniform(n)+1;
col = StdRandom.uniform(n)+1;
}
perc.open(row, col);
count++;
}
perc = null;
results[i] = count/(n * n * 1.0);
}
mean = StdStats.mean(results);
stddev = StdStats.stddev(results);
confidenceLo = mean - 1.96 * stddev / Math.sqrt(trials);
confidenceHi = mean + 1.96 * stddev / Math.sqrt(trials);
}
// sample mean of peration threshold
public double mean()
{
return mean;
}
// sample standard deviation of percolation threshold
public double stddev()
{
return stddev;
}
// low endpoint of 95% confidence interval
public double confidenceLo()
{
return confidenceLo;
}
// high endpoint of 95% confidence interval
public double confidenceHi()
{
return confidenceHi;
}
public static void main(String[] args)
{
int n = Integer.parseInt(args[0]);
int trials = Integer.parseInt(args[1]);
PercolationStats stats = new PercolationStats(n, trials);
System.out.println("mean\t= " + stats.mean());
System.out.println("stddev\t= " + stats.stddev());
System.out.println("95% confidence interval = [" + stats.confidenceLo() + ", " + stats.confidenceHi() + "]");
}
}